일반 물리학 Chapter 8. 에너지의 보존
*본 포스팅은 Serway 물리학교재 번역본 <대학물리학> 9판을 정리한 내용입니다. *
8.1 분석 모형 : 비고립계 (에너지)
일 (work) : 7장에서 살펴본 바와 같이 계에 작용하는 힘과 힘의 작용점의 변위에 의하여 에너지가 전달되는 방법이다.
역학적 파동(mechanical waves, 16~18장) : 공기나 다른 매질을 통하여 교란(disturbance)함으로써 에너지를 전달하는 방법이다.
열(heat, 20장) : 계와 주위 환경 사이의 온도 차이에 의하여 에너지를 전달하는 메커니즘이다.
물질 전달 (matter transfer, 20장) : 물질을 물리적으로 계의 경계를 넘게 하여 물질과 함께 직접적으로 에너지를 전달하는 방법이다.
전기 송전 (electrical transmission, 27,28장) : 전류를 매개로 하여 계 내부로 또는 계로부터 외부로 에너지를 전달하는 방법이다.
전자기 복사 (electromagnetic radiation. 34장) : 빛, 마이크로파 그리고 라디오파와 같은 전자기파를 매개로 하여 계의 경계를 넘어 에너지를 전달하는 방법이다.
계의 전체 에너지가 변한다면, 그 이유는 오직 앞에서 나열한 에너지 전달 방법 중 하나와 같은 에너지 전달 방식으로 에너지가 계의 경계를 넘기 때문이다.
에너지는 물리학에서 보존되는 양 중의 하나이다. 이 일반적인 에너지 보존(conservation of energy)의 원리를 수학적으로 표현한 에너지 보존 식은 다음과 같다.
\[\Delta E_{system} = \sum T \qquad (8.1)\]여기서 \(E_{system}\)은 계의 전체 에너지로서 계에 저장할 수 있는 모든 에너지(운동 에너지, 퍼텐셜 에너지, 그리고 내부 에너지)를 나타내고, \(T\)는 어떤 전달 메커니즘을 거치면서 계의 경계를 넘어 전달되는 에너지양이다.
전달 메커니즘을 수학적 기호로 표현해 식 8.1을 완전히 전개하면 다음과 같다.
\[\Delta K + \Delta U + \Delta E_{int} = W + Q + T_{MW} + T_{MT} + T_{ET} + T_{ER} \qquad (8.2)\]이것은 비고립계(nonisolated system) 에너지르 분석 모형의 주요한 수학적인 표현이다.
만일 주어진 계에 대하여 에너지 보존 식의 우변의 모든 항들이 0인 경우, 계는 고립계이고 다음 절에서 다룬다.
8.2 분석 모형 : 고립계(에너지)
앞 장의 그림 7.14의 책-지구 계를 생각해보자.
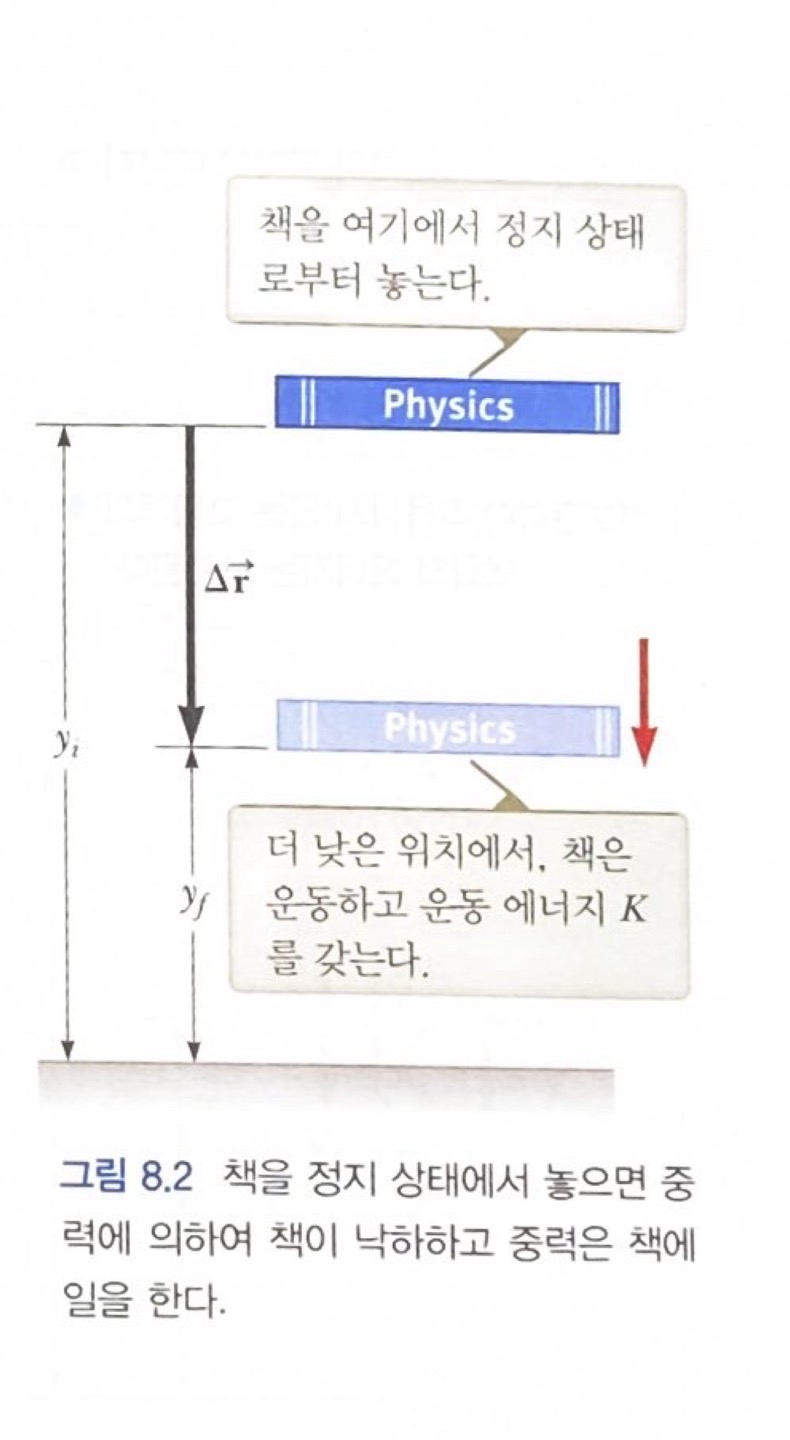
들어 올렸던 책이 원래 위치로 되돌아올 때 중력이 책에 한 일에만 초점을 맞추어 보자. 책이 \(y_i\)에서 \(y_f\)로 낙하할 때 중력이 책에 한 일은
\[W_{on book} = (m\vec g) \cdot \Delta \vec r = (-mg\hat j) \cdot [(y_f-y_i)\hat j] = mgy_i - mgy_f \qquad (8.3)\]7장의 일-운동 에너지 정리에 따르면, 책에 한 일은 책의 운동 에너지의 변화와 같다.
\[W_{on book} = \Delta K_{book}\]책에 한 일에 대한 두 식을 같게 놓을 수 있으므로
\[\Delta K_{book} = mgy_i - mgy_f \qquad (8.4)\]이다. 이 제 위 식의 양변을 책과 지구로 구성된 계와 관련지어 보자. 우변은
\[mgy_i - mgy_f = -(mgy_f - mgy_i) = -\Delta U_g\]이고, 여기서 \(U_g\)는 중력 퍼텐셜 에너지이다. 식8.4의 좌변은 책이 계에서 유일하게 움직이는 부분이므로 \(\Delta K_{book} = \Delta K\)이고, 여기서 \(K\)는 계의 운동 에너지이다. 그러므로 식 8.4의 각 변을 책 - 지구 계에 해당하는 양으로 대치하면
\[\Delta K = -\Delta U_g \qquad (8.5)\]가된다. 앞의 식을 중력 퍼텐셜 에너지가 있는 하나의 중력계에서 유도하였지만, 다른 형태의 퍼텐열 에너지를 갖는 계에서도 유도할 수 있다. 그러므로 한 고립계에 대해 다음이 성립.
\[\Delta K + \Delta U = 0 \qquad (8.6)\]7장에서 계의 역학적 에너지를 운동 에너지와 퍼텐셜 에너지의 합이라 정의하였다.
\[E_{mech} = K + U \qquad (8.7)\]지금 고려하고 있는 계가 고립계이므로, 식 8.6과 8.7은 역학적 에너지가 보존됨을 알 수 있다.
\[\Delta E_{mech} = 0 \qquad (8.8)\]식 8.8은 계에 비보존력이 작용하지 않는 고립계에 대한 역학적 에너지의 보존(conservation of mechanical energy)을 표현한 식이다.
8.3 운동 마찰이 포함되어 있는 상황
마찰력 외의 물체에 작용하는 다른 힘들에 대하여 식 7.8 (\(\sum W = W_{ext} = \int (\sum \vec F) \cdot d \vec r\))을 써보자.
\[\sum W_{other forces} = \int (\sum \vec F_{other forces}) \cdot d \vec r \qquad (8.11)\]이를 다음과 같이 사용하는데 유용하다.
\[\begin{align} \sum W_{other forces} + \int \vec f_k \cdot \vec r &= \int (\sum \vec F_{other forces}) \cdot d \vec r + \int \vec f_k \cdot d \vec r \\ &= \int (\sum \vec F_{other forces} + \vec f_k) \cdot d \vec r \end{align}\]우변의 괄호 속은 물체에 작용하는 알짜힘 \(\sum \vec F\)이므로
\[\sum W_{other forces} + \int \vec f_k \cdot d \vec r = \int \sum \vec F \cdot d \vec r\]이다. 여기서 뉴턴의 제 2법칙을 적용하면
\[\begin{align} \sum W_{other force} + \int \vec f_k \cdot d \vec r &= \int m \vec a \cdot d \vec r \\ &= \int m \frac{d \vec v}{dt} \cdot d \vec r = \int_{t_i}^{t_f} m \frac{d\vec v}{dt} \cdot \vec v dt \end{align}\](4)에서 미분 연쇄 법칙을 이용하였다.
\[\frac {d}{dt} (\vec v \cdot \vec v) = \frac {d \vec v}{dt} \cdot \vec v + \vec v \cdot\frac {\vec dv}{dt} = 2 \frac {d \vec v}{dt} \cdot \vec v\] \[\frac{d \vec v}{dt} \cdot \vec v = \frac 12 \frac {d}{dt} (\vec v \cdot \vec v) = \frac 12 \frac {dv^2}{dt}\]이를 (4)에 대입하면
\[\begin{align} \sum W_{other forces} + \int \vec f_k \cdot d \vec r &= \int_{t_i}^{t_f}m(\frac 12 \frac {dv^2} {dt}) dt \\ &= \frac 12 m \int_{t_i}^{t_f}d(v^2) = \frac{1}{2}mv^2_f - \frac 12 m v^2_i = \Delta K \end{align}\]이다. 식의 좌변에서 관성틀 표면에서 볼 때, 물체 경로에 있는 모든 변위 요소 \(d \vec r\)에 대해 \(\vec f_k\)와 \(d \vec r\)는 반대 방향이다. 그래서 \(\vec f_k \cdot d \vec r = -f_k dr\)이므로 위 식은
\(\sum W_{other forces} - \int f_k dr = \Delta K\) 가 된다. 마찰에 대한 모형에서 운동 마찰력 크기가 일정하므로 식을 정리하면
\[\sum W_{other forces} - f_kd = \Delta K \qquad (8.13)\]식 8.13은 물체에 마찰력이 작용할 때 사용할 수 있다.
일정한 마찰력에 의한 계의 내부 에너지 변화식은 다음과 같다.
\[-f_kd + \Delta E_int = 0\] \[\Delta E_{int} = f_k d \qquad (8.14)\]식 8.14를 이용하면 식 8.13에서 마찰 이외의 힘들이 계에 한 일은 다음과 같이 쓸 수 있다.
\[\sum W_{other forces} = W = \Delta K + \Delta E_{int} \qquad (8.15)\]8.4 비보존력에 의한 역학적 에너지의 변화
예를 들어 책이 마찰이 있는 경사면 위를 따라 이동한다면, 책-지구 계의 운동 에너지 뿐만 아니라 퍼텐셜 에너지 모두에 변화가 생긴다. 결과적으로
\[\Delta E_{mech} = \Delta K + \Delta U_g = -f_kd = -\Delta E_{int}\]이 식을 일반화하면 고립계에서 비보존력이 작용 시
\[\Delta K + \Delta U + \Delta E_{int} = 0 \qquad (8.16)\]비고립계 안에서 다른 비보존력이 작용하고 계에 작용하는 외부 영향이 일의 형태로 주어진다고 하면, 식 8.13을 일반화하여
\[\sum W_{other forces} - f_kd = \Delta E_{mech}\]가 되고, 식 8.7과 8.14를 이용하면 이 식은
\[\sum W_{other forces} = W = \Delta K + \Delta U + \Delta E_{int} \qquad (8.17)\]로 쓸 수 있다.
8.5 일 률
에너지 전달의 시간에 대한 비율을 순간 일률(instantaneous power) \(P\)라 하고 다음과 같이 정의한다.
\[P \equiv \frac{dE}{dt} \qquad (8.18)\]외력이 작용하는 시간 \(\Delta t\) 동안에 물체에 한 일을 \(W\)라고 한다면, 이 시간 동안의 평균 일률(average power)은
\[P_{avg} = \frac {W}{\Delta t}\]속도와 가속도를 정의할때 적용한 방식과 유사하게, 순간 일률은 \(\Delta t\)가 0에 접근할 때의 평균 일률의 극한이다.
\[P = \lim_{\Delta t \to 0} \frac {W}{\Delta t} = \frac {dW}{dt}\]여기서 매우 작은 일을 \(dW\)로 표시하였다. \(W = F\Delta r cos \theta = \vec F \cdot \Delta \vec r\)이므로 \(dW = \vec F \cdot d \vec r\) 로 주어진다. 그러므로 순간 일률은
\[P = \frac {dW}{dt} = \vec F \cdot \frac {d \vec r}{dt} = \vec F \cdot \vec v \qquad (8.19)\]로 쓸 수 있고, 여기서 \(\vec v = \frac {d \vec r} {dt}\) 이다.
일률의 SI 단위는 줄/초(j/s)이고, 와트(James Watt)의 업적을 기리기 위하여 와트(watt , W)라고 한다.
\[1 W = 1 J/s = 1kg \cdot m^2/s^3\]미국 관습 단위계에서 일률의 단위는 마력(horsepower, hp)이다.
에너지(또는 일)의 단위를 일률의 단위로 표시할 수도 있다. 1킬로아트-시(kWh)는 1 kW = 1 000 J/s인 일정한 일률로 한 시간 동안 전달된 에너지 양으로
\[1 kWh = (10^3 W)(3 600s) = 3.60 \times 10^6J\]