일반 물리학 Chapter 7.계의 에너지
*본 포스팅은 Serway 물리학교재 번역본 <대학물리학> 9판을 정리한 내용입니다. *
7.1 계와 환경
계의 유효한 정의
- 하나의 물체 또는 입자일 수 있다.
- 물체나 입자들의 집합일 수 있다.
- 공간의 일부 영역일 수 있다(예를 들어 자동차 엔진의 연소 실린더 내부).
- 시간에 따라 크기와 모양이 변할 수 있다.(예를 들어 벽에 부딪쳐서 형태가 변하는 고무공).
주어진 문제에서 특정한 계가 무엇이든 간에, 계의 경계(system boundary)라는 가상의 면이 있는데, 이 면은 우주를 계와 그 계를 둘러싼 환경(environment)으로 나눈다.
7.2 일정한 힘이 한 일
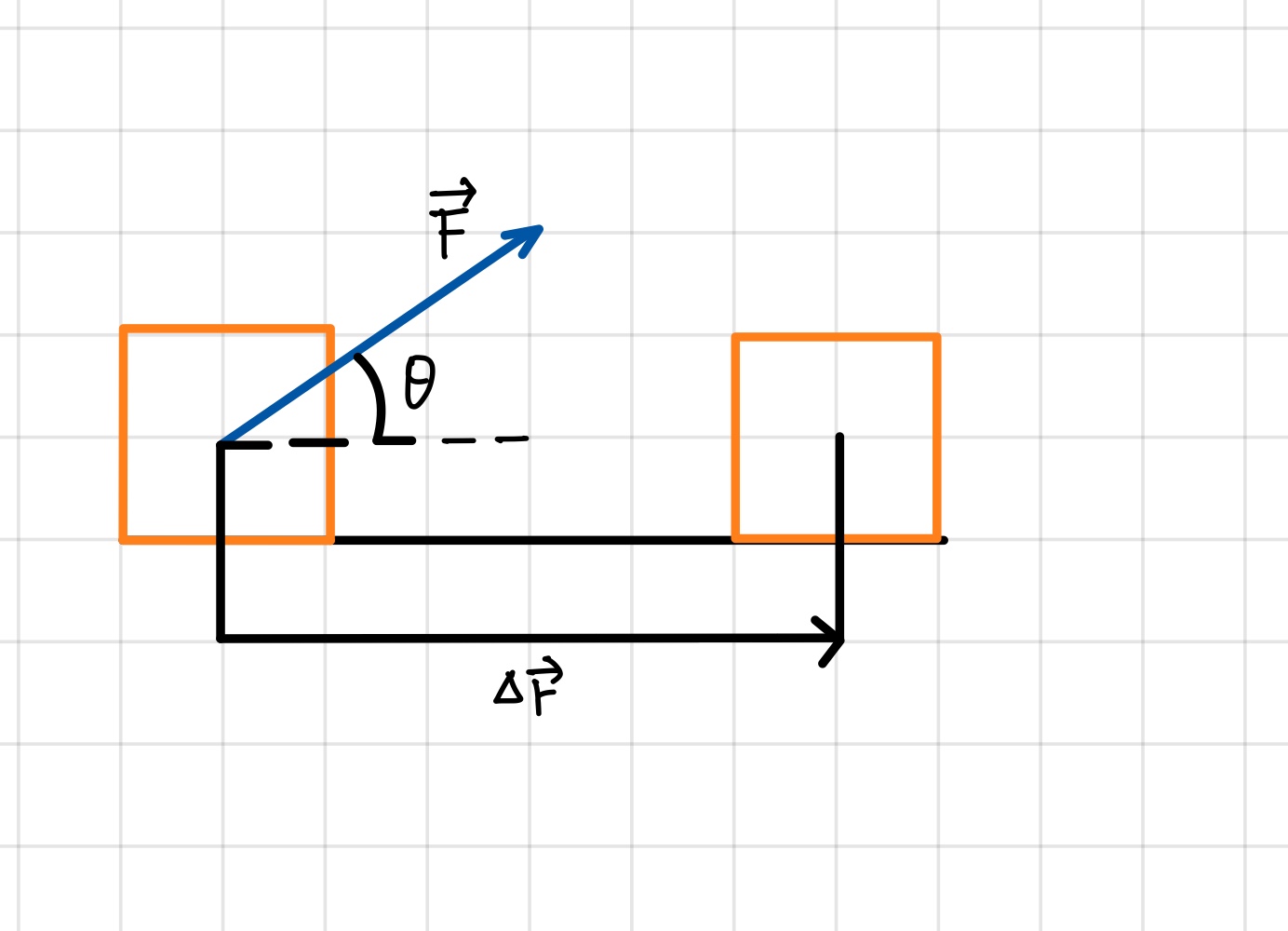그림 7.2 에서 물체(계)는 직선 상에서 위치가 변하는데, 크기가 \(F\)인 일정한 힘이 변위의 방향과 각도 \(\theta\)를 이루며 작용한다.
어떤 계의 일정한 크기의 힘을 가하는 주체가 계에 한 일(work) \(W\)는 힘의 크기 \(F\), 힘의 작용점의 변위 크기 \(\Delta r\)그리고 \(cos \theta\)의 곱이다. 여기서 \(\theta\)는 힘과 변위 벡터가 이루는 각도이다.
\[W = F \Delta r cos\theta \qquad (7.1)\]식에서 일이 두 벡터에 의해 정의 되지만, 일은 스칼라양임을 주목하자.
또한 식에서 변위는 힘의 작용점의 변위임에 주목한다.
그리고 움직이는 물체에 작용한 힘이 작용점의 변위에 대하여 수직이라면 그 힘이 한 일은 0이란 것에 주목한다. 즉 \(\theta = \frac{\pi}{2}\) 이면 \(cos\frac \pi 2 = 0\) 이므로 \(W = 0\)인 것이다.
일의 부호는 또한 \(\Delta \vec r\)에 대한 \(\vec F\)의 방향에도 의존한다. 작용한 힘이 한 일은 \(\Delta \vec r\)에 대한 \(\vec F\)의 사영이 변위의 방향과 같을 때 \((+)\)이다. 반대일 경우 \((-)\)이다. 식 7.1 에서 \(cos\theta\)가 자동적으로 일의 부호를 결정한다.
작용한 힘 \(\vec F\)가 변위 \(\Delta \vec r\)와 같은 방향이라면 \(\theta = 0\) 이고 \(cos0 = 1\)이다. 이 경우 식 7.1은 다음과 같다.
\[W = F\Delta r\]일의 단위는 힘에 길이를 곱한 것이다. 따라서 일의 SI단위는 뉴턴·미터(\(N · m = kg · m^2 / s^2\))이다. 이 단위의 조합은 자주 사용되므로 줄(\(J\))이라는 공한 이름을 붙였다.
계를 사용하여 문제를 해경하기 위하여 고려해야 할 중요한 점은 일은 에너지의 전달 이라는 것이다.
7.3 두 벡터의 스칼라곱
식 7.1과 같이 힘과 변위 벡터가 조합을 이루므로, 두 벡터의 스칼라곱(scalar product)이라는 간편한 수학적 도구를 사용하면 도움이 된다.
벡터 \(\vec A\) 와 \(\vec B\)의 스칼라곱은 \(\vec A \cdot \vec B\)로 쓰기로 한다. 도트 (dot) 부호를 사용하므로 도트곱 (dot product)이라고도 한다.
식 7.1을 스칼라곱 형태로 바꾸면 다음과 같다. \(W = F\Delta r cos \theta = \vec F \cdot \Delta \vec r \qquad (7.2)\)
스칼라곱은 교환 법칙과 분배 법칙이 성립한다.
7.4 변하는 힘이 한 일
위치에 따라 변하는 힘의 작용을 받아 \(x\) 축으로 움직이는 입자를 생각해 보자.
이 상황에서는 힘이 한 일을 식 7.1로 계산할 수 없는데, 그 이유는 이 식이 \(\vec F\)의 크기와 방향이 변하지 않을 때에만 적용되기 때문이다.
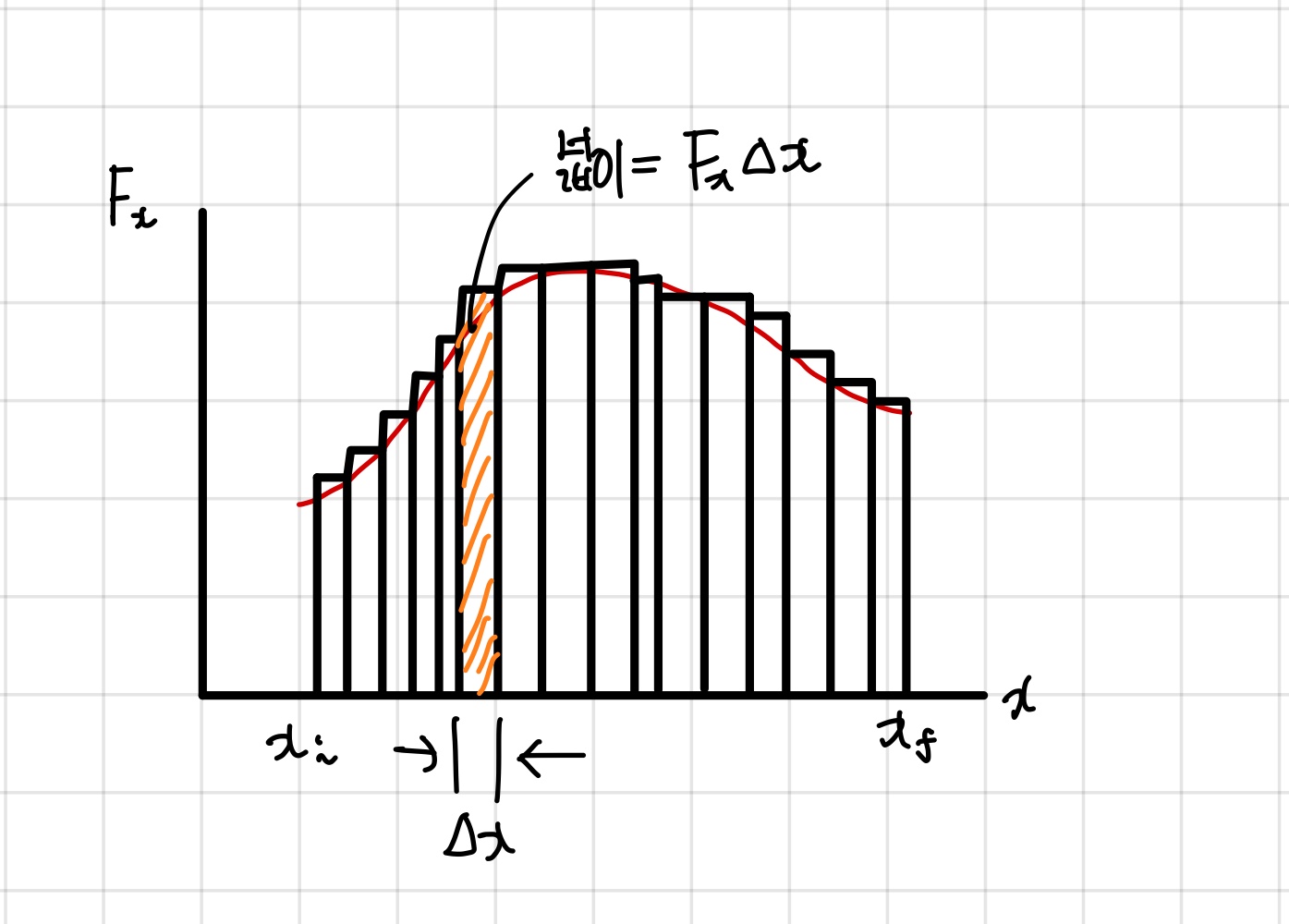그림에서 처음 위치 \(x_i\) 에서 나중 위치 \(x_f\)로 이동하는 입자에 작용하는 변하는 힘을 보여준다.
이 그림에서와 같이 매우 작은 \(\Delta x\) 만큼의 변위만이 있었다고 가상한다면, 이 작은 구간에 대해 힘의 \(x\)성분인 \(F_x\)는 근사적으로 일정하다. 이 작은 변위에 대해 이 힘이 한 일은 식 7.1을 이용해 \(W \approx F_x \Delta x\) 로 근사적으로 쓸 수 있다. 이 값은 그림에 나타난 색칠한 사각형의 넓이이다.
만약 \(F_x - x\) 곡서능ㄹ 동일한 간격으로 많이 나눈다면, \(x_i\) 에서 \(x_f\)로의 변위 동안 일의 전체합은 근사적으로 다음과 같은 많은 항의 합으로 쓸 수 있다.
\[W \approx \displaystyle \sum _{x_i} ^{x_f} {F_x \Delta x}\]만약 작은 구간의 크기 \(\Delta x\)를 0에 접근시킬 수 있다면, 위의 합에 사용될 항의 개수는 무한히 늘어나지만 합의 값은 다음과 같이 \(F_x\) 곡선과 \(x\) 축사이의 넓이와 같은 값이 된다.
\[\displaystyle \lim _{\Delta x \to 0} \sum _{x_i} ^{x_f} F_x \Delta x = \int _{x_i} ^{x_f} F_x dx\]따라서 입자계가 \(x_i\) 에서 \(x_f\)로 움직일 떄 \(F_x\)가 한 일은
\[W = \int _{x_i} ^{x_f} {F_x} dx \qquad (7.3)\]식 7.3은 힘의 성분 \(F_x = Fcos\theta\)가 일정하다면 식 7.1이 된다.
어떤 계에 하나 이상의 힘이 작용하고 그 계를 입자로 모형화할 수 있다면, 그 계에 대하여 한 전체 일은 알짜힘이 한 일과 같다. x방향으로의 알짜힘을 \(\Sigma F_x\) 라고 하면,입자가 \(x_i\)에서 \(x_f\)로 움직일 때, 전체 일 또는 알짜일은 다음과 같다.
\[\sum W = W_{ext} = \int_{x_i}^{x_f} {(\sum F_x)}dx \quad (입자)\]보다 일반적인 경우로서 알짜힘이 \(\Sigma \vec F\) 이고 크기와 방향이 모두 변하는 경우, 스칼라곱을 사용하여 다음과 같이 쓸 수 있다.
\[\sum W = W_{ext} = \int_{}^{} {(\sum \vec F)} \cdot d\vec r \quad (입자) \qquad (7.4)\]식(7.4)은 입자가 공간에서 움직이는 경로에 대하여 계산하는 것이다. 일에 붙인 아래 첨자 ‘ext’는 외부에서 계에 알짜일을 하였다는 뜻이다. 이 장에서는 내부 일과 이 일을 구분하기 위해 이 기호를 사용한다.
계를 입자로 모형화할 수 없는 경우, 식 7.4를 이용할 수 없다. 왜냐면 계에 작용하는 서로 다른 힘에 대한 변위가 각기 다를 수 있기 때문이다. 이 경우는 각각의 힘이 한 일을 따로 구하고, 그것을 산술적으로 다시 더해야 알짜일을 구할 수 있다.
\[\sum W = W_{ext} = \sum _{forces}(\int \vec F \cdot d\vec r) \qquad (변형가능한"계") \qquad (7.5)\]용수철이 한 일
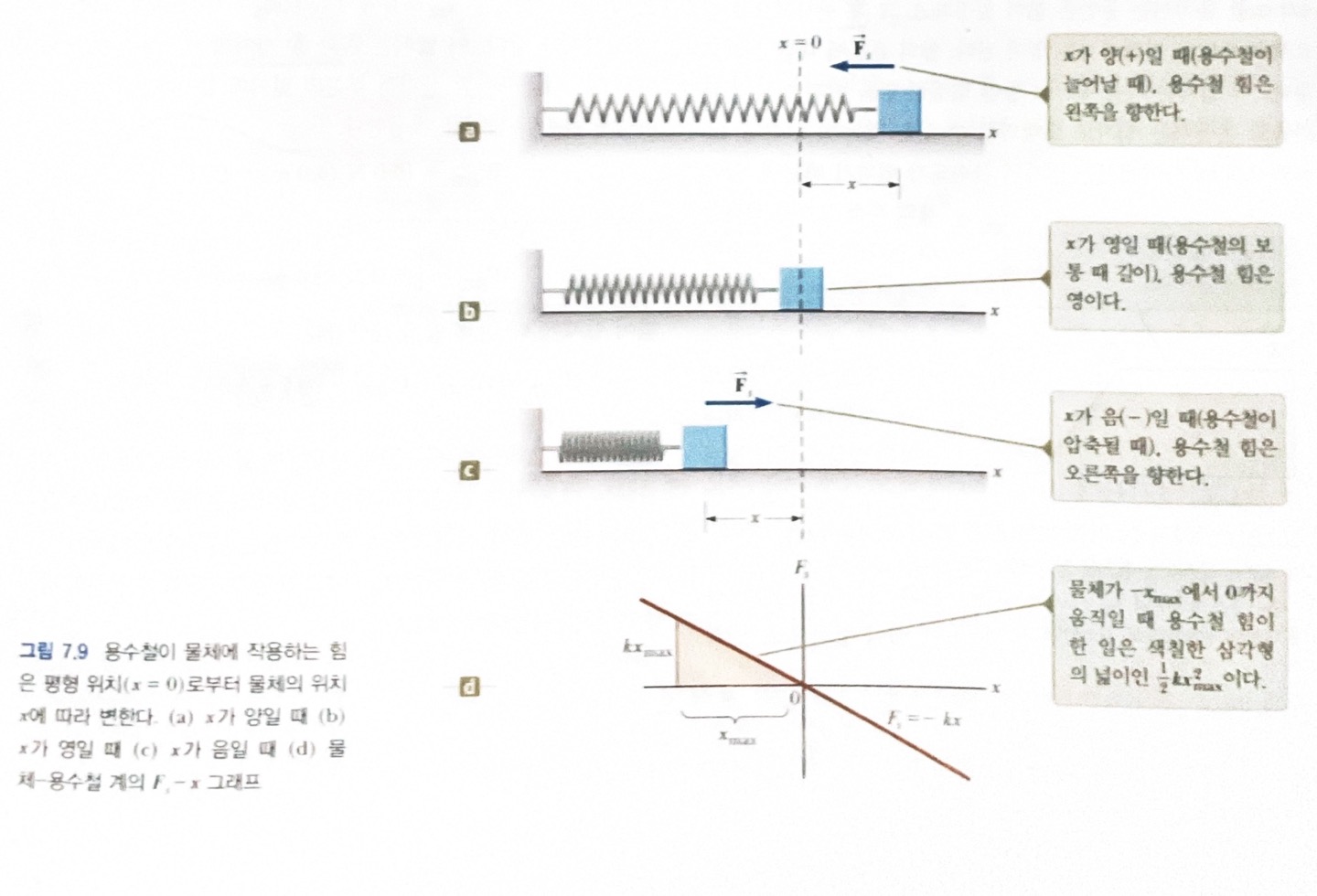그림은 위치에 따라 힘이 변하는 통상적인 물리계의 모형이다. 수평이며 마찰이 없는 면 위에 용수철에 연결된 물체가 있다. 용수철이 늘어나지 않은 상태, 즉 평형 상태에서 작은 거리만큼 늘어나거나 줄어들면 용수철이 물체에 작용하는 힘은 다음과 같다.
여기서 \(x\)는 평형 상태(\(x = 0\))에 대한 물체의 위치이고, \(k\)는 용수철의 힘 상수(force constant) 또는 용수철 상수(spring constant)라고 하는데, 양수이다. 다시 말하면 용수철을 늘이거나 압축시킬 때 필요한 힘은 늘어나거나 줄어든 길이 \(x\)에 비례한다.
용수철의 힘에 관한 이 법칙은 \(훅의 법칙\)(Hooke’s law)이라고 한다.
\(k\)의 값은 용수철의 탄성을 나타낸다. 단단한 용수철은 \(k\)값이 크고, 무른 용수철은 작다. 식 7.6에서 알 수 있듯이 \(k\)의 단위는 N/m 이다.
식 7.6를 벡터 형식으로 쓰면 다음과 같다. \(\vec F_s = F_s \hat i = -kx \hat i \qquad (7.7)\)
여기서 \(x\)축은 용수철이 늘어나거나 압축된느 방향과 나란하도록 선택하였다.
식 7.6와 7.7에서 음(-)의 부호는 용수철 힘이 언제나 평형 위치로부터의 변위에서 반대 방향이라는 것을 의미한다. 용수철 힘은 항상 평형 위치(\(x = 0\))로 향하기 때문에 복원력이라고 한다.
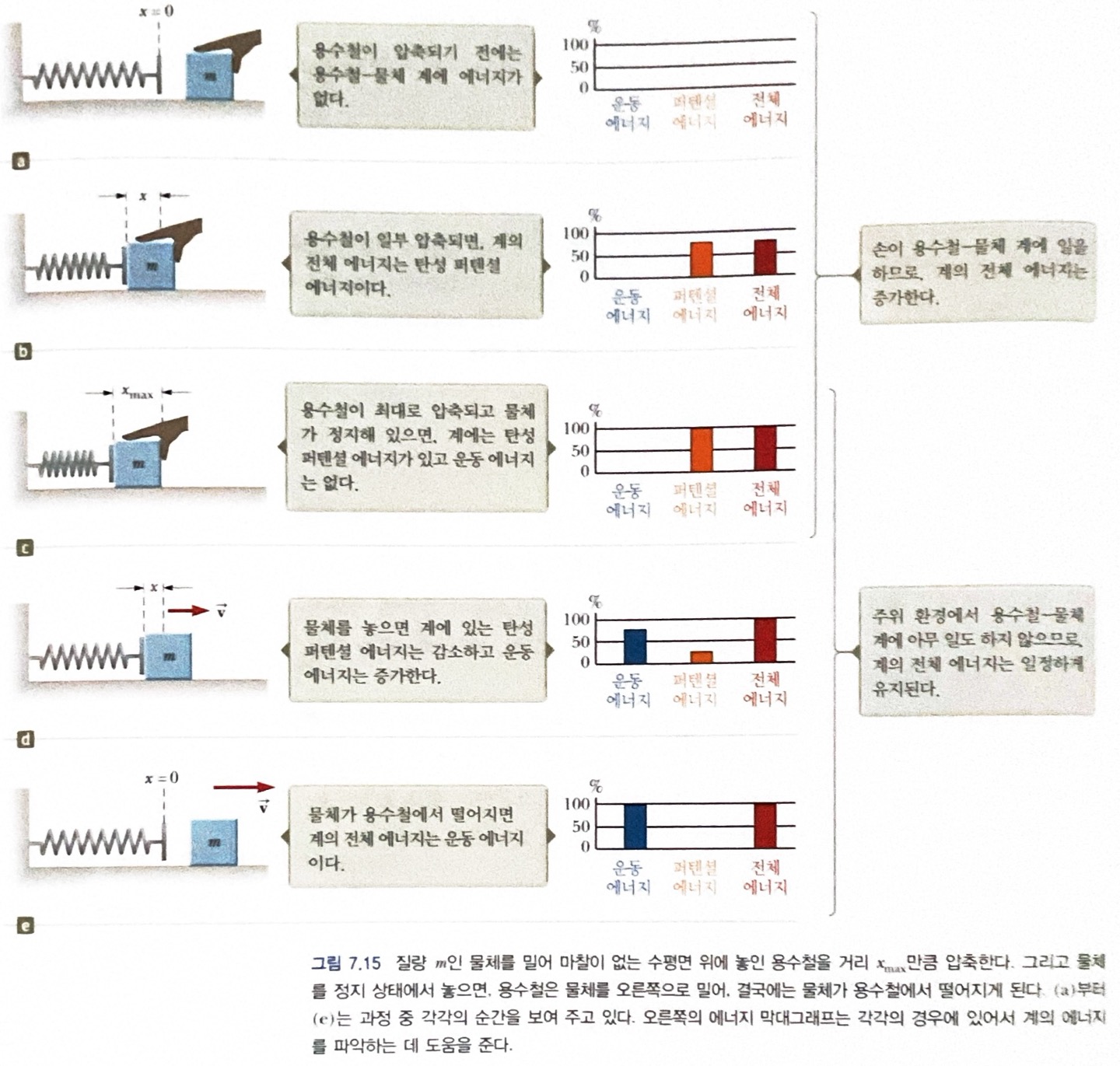
물체를 \(-x_{max}\)까지 왼쪽으로 밀어 놓은 경우를 생각해 보자. 물체만을 계라고 정하고 \(x_i = -x_{max}\)에서 \(x_f = 0\)까지 물체가 움직일 때, 용수철이 물체에 한 일 \(W_s\)를 계산해 보자. 식 7.5를 적용하고 물체를 입자로 취급할 수 있다고 가정하면, 일은 다음과 같다.
\[W_s = \int \vec F_s \cdot d\vec r = \int _{x_i} ^{x_f} {(-kx \hat i) \cdot (dx\hat i)} = \int_{-x_{max}}^{0} (-kx)dx = \frac 12 k x^2_{max} \qquad (7.8)\]용수철 힘이 한 일은 양(+)인데, 이것으 힘이 물체의 변위와 같은 방향이기 때문이다. (둘다 오른쪽)
물체가 \(x = 0\)에 도달할 떄 속력이 0이 아니므로 물체는 \(+x_{max}\)에 도달할 때까지 계속 움직인다.
물체가 \(x_i = 0\) 에서 \(x_f = x_{max}\)까지 움직이는 동안 용수철 힘이 물체에 한 일은 \(W_s = -\frac12 kx^2_{max}\)이다.
이 부분의 운동에서 용수철 힘의 방향은 왼쪽이고 변위의 방향은 오른쪽이기 때문에 일음 음이다. 따라서 \(x_i = -x_{max}\) 에서 \(x_f = +x_{max}\)까지 물체가 움직이는 동안 용수철 힘이 한 알짜일은 0이다.
그림의 d는 \(F_s - x\) 그래프이다. 식 7.8에서 구한 일은 색칠한 삼각형의 넓이로, \(-x_{max}\)에서 \(0\)까지의 변위에 대한 것이다. 삼각형의 밑변은 \(x_{max}\)이고 높이는 \(kx_{max}\)이므로 넓이는 \(\frac 12 k x^2_{max}\)이고, 이는 식 7.8에서 구한 용수철이 한 일과 일치한다.
물체가 \(x = x_i\)에서 \(x = x_f\)까지 임의의 변위를 움직인다면, 용수철 힘이 물체에 한 일은 다음과 같다.
\[W_s = \int _{x_i} ^{x_f} (-kx)dx = \frac 12 k x^2_i - \frac 12 k x^2_f \qquad (7.9)\]식 7.9를 통해 알 수 있는 것은 시작점이 끝점이 되는 운동에 대해서도 용수철힘이 한 일은 0이라는 것이다.
식 7.8과 7.9는 용수철 힘이 물체에 한 일이다.
이제 외력이 작용하여 물체를 \(x_i = -x_{max}\)에서 \(x_f = 0\)까지 매우 천천히 움직이도록 한 경우 그 힘이 물체에 한 일을 생각해보자.
어느 위치에서든지 이 외력 \(\vec F_{app}\)는 용수철 힘 \(\vec F_s\)와 크기는 같고 방향은 반대이므로 \(\vec F_{app} = F_{app} \hat i = -\vec F_s = -(-kx\hat i) = kx\hat i\)라는 것에 주목하면 그 일을 구할 수 있다.
따라서 외력이 물체의 계에 한 일은 다음과 같다.
\[W_{ext} = \int \vec F_{app} \cdot d\vec r = \int_{x_i}^{x_f}(kx\hat i) \cdot (dx\hat i) = \int_{-x_{max}}^{0} kx dx = -\frac 12 kx^2_{max}\]이 일은 같은 변위에 대하여 용수철 힘이 한 일의 음(-)과 같다.
그 이유는 물체가 \(-x_{max}\)에서 0까지 움직이는 동안 외력이 용수철이 늘어나지 못하도록 안쪽으로 밀어 주어 그 방향이 힘의 작용점의 변위와 반대가 되기 때문이다.
물체가 \(x = x_i\) 에서 \(x = x_f\)까지 움직이는 동안 (용수철 힘이 아닌) 외력이 계에 한 일은
\[W_{ext} = \int_{x_i}^{x_f}kxdx = \frac 12 kx_f^2 - \frac 12 kx_i^2 \qquad (7.10)\]이 식은 식 7.9의 음(-)과 같다.
7.5 운동 에너지와 일-운동 에너지 정리
계가 가질 수 있는 에너지의 첫 번쨰 형태인 운동 에너지를 소개한다.
단일 물체로 이루어진 계를 생각해보자.
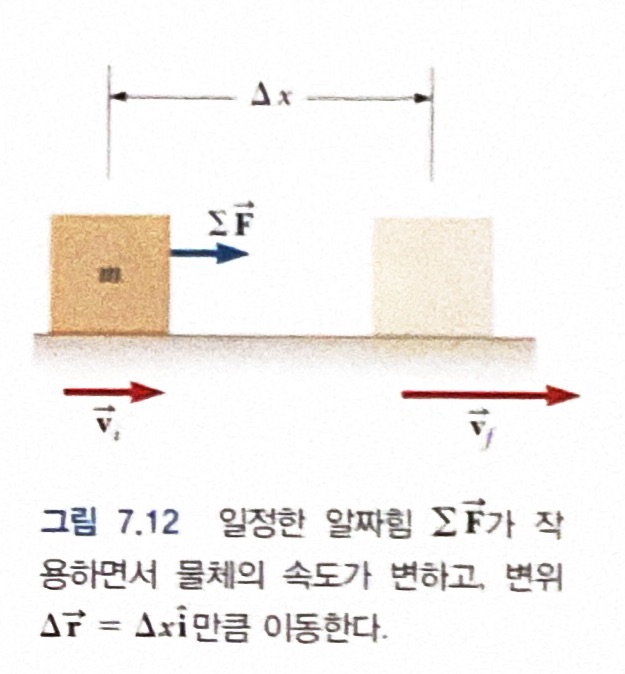그림에서 물체의 움직이는 변위가 \(\Delta \vec r = \Delta x \hat i = (x_f - x_i) \hat i\)이라면, 알짜힘 \(\Sigma \vec F\)가 한 일은 다음과 같다.
뉴턴의 제2법칙을 이용해 알짜힘의 크기를 \(\Sigma F = ma\)로 대입한 후 다음의 연쇄 법칙을 적분에 활용하자.
\[W_{ext} = \int_{x_i}^{x_f} ma dx = \int_{x_i}^{x_f} m \frac {dv}{dt}dx = \int_{x_i}^{x_f} m \frac {dv}{dx} \frac {dx}{dt}dx = \int_{v_i}^{v_f}mv dv\] \[W_{ext} = \frac 12 mv_f^2 - \frac 12 mv_i^2 \qquad (7.12)\]이때 알짜힘이 질량 \(m\)인 입자에 한 일은 \(\frac 12 mv^2\)의 처음값과 나중 값의 차이와 같다. 이는 매우 중요한 양으로 특별히 운동 에너지(kinetic energy)라 부른다.
\[K \equiv \frac 12 mv^2 \qquad (7.13)\]식 7.12는 다음 형태로 나타내는 것이 편리할 경우도 있다.
\[W_{ext} = K_f - K_i = \Delta K \qquad (7.14)\]\(K_f = K_i + W_{ext}\) 로 쓸 수 있으며, 나중 운동 에너지는 처음 운동 에너지에 알짜힘이 한 일을 더한 것과 같다.
식 7.14는 중요한 결과이며 일-운동 에너지 정리(work_kinetic energy theorem)라고 한다.
어떤 계에 일이 가해지고 계의 유일한 변화가 속력이라면, 계에 한 알짜일은 식 7.17에서 \(W = \Delta K\)로 표현한 것처럼 계의 운동 에너지의 변화와 같다.
일-운동 에너지 저이에 의하면 행해진 알짜일의 부호가 양(+)이면 어떤 계의 속력은 증가하는데, 그 이유는 나중 운동 에너지가 처음 운동 에너지보다 크기 때문이다. 알짜일이 음(-)이면 속력은 감소하는데, 이것은 나중 운동 에너지가 처음 운동 에너지보다 작기 때문이다.
7.6 계의 퍼텐셜 에너지
중력으로 상호 작용을 하는 책과 지구로 된 계를 생각해 보자.
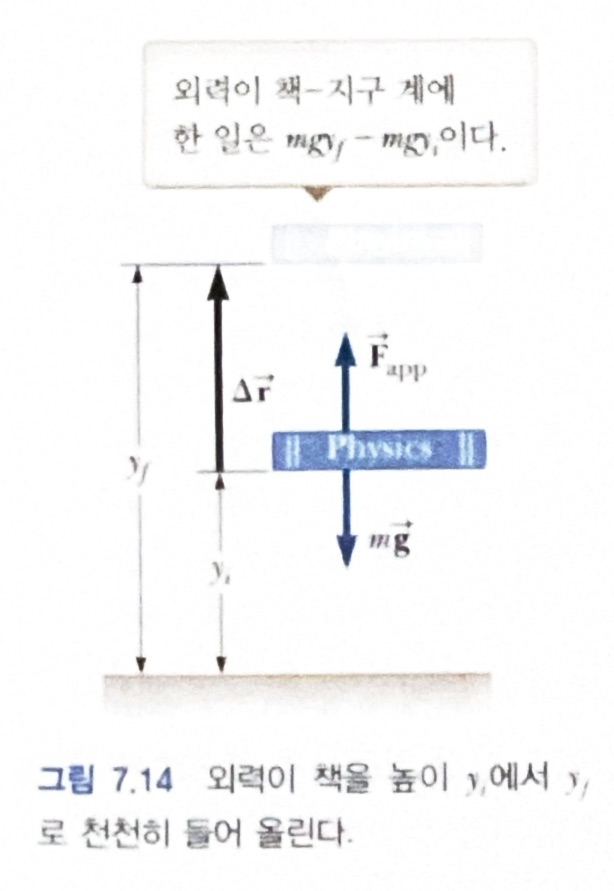책을 들어 올린 후 놓으면, 원래 위치 \(y_i\)로 낙하한다. 이 때 책은 운동에너지를 가지며, 그 에너지는 책을 들어 올릴떄 한 일에서 온 것임에 주목하자. 책이 가장 높은 위치에 있을 때, 계에는 운동 에너지로 바뀔 수 있는 잠재적인 에너지가 있고, 이것은 책이 떨어지면서 운동 에너지로 바뀌게 된 것이다. 책을 놓기 전의 이런 에너지 저장 형태를 퍼텐셜 에너지(potential energy)라 한다. 퍼텐셜 에너지의 크기는 계의 구성요소들의 배열 상태에 따라 결정된다.
지표면 위로 특정한 위치에 놓인 물체와 관련된 퍼텐셜 에너지 식을 유도하자. 그림의 상황을 적용하면 외력이 계에 한 일은 다음과 같다.
\[W_{ext} = (\vec F_app) \cdot \Delta \vec r = (mg\hat j) \cdot [(y_f-y_i)\hat j] = mgy_f - mgy_i \qquad (7.15)\]여기서 \(mgy\)를 중력 퍼텐셜 에너지(gravitational potential energy) \(U_g\)로 정의할 수 있다.
\[U_g \equiv mgy \qquad (7.16)\]이를 이용해 식 7.15를 다시쓰면
\[W_{ext} = \Delta U_g\]이는 외력들이 계에 한 알짜일은 운동 에너지의 변화가 없을 때 계의 중력 퍼텐셜 에너지의 변화로 나타남을 수학적으로 표현한 것이다.
탄성 퍼텐셜 에너지
계가 가질 수 있는 두 번째 형태의 퍼텐셜 에너지를 생각해보자.
용수철이 물체에 작용하는 힘은 \(F_s = -kx (7.9)\)이다. 외력 \(F_{app}\)가 용수철-물체 계에 한 외부 일은 식 7.10으로 주어진다.
여기서 물체의 처음과 나중 \(x\) 좌표를 평형 위치 \((x = 0)\)으로 부터 측정한다. 중력의 경우와 마찬가지로 외력이 계에 한 일은 계의 배열과 관련된 어떤 양의 처음과 나중 값의 차이와 같다. 물체-용수철 계에서의 탄성 퍼텐셜 에너지(elastic potential energy)함수는
\(U_s \equiv \frac 12 kx^2 \qquad (7.19)\) 로 정의한다. 식 7.18은 다음과 같이 표현 가능하다.
\[W_{ext} = \Delta U_s\]이 식을 식 7.14 그리고 7.17과 비교해보자. 세 경우 모두, 계에 일을 하면 그 결과로 계 내에 저장된 에너지의 형태가 변한다.
7.7 보존력과 비보존력
계가 가질 수 있는 세번쨰 종류의 에너지를 살펴보자.
보존력
보존력은 두 가지 성질이 있다.
- 두 점 사이를 이동하는 입자에 보존력이 한 일은 이동 경로와 무관한다.
- 닫힌 경로를 따라 이동하는 입자에 보존력이 한 일은 영이다(닫힌 경로는 출발점과 도착점이 같은 경로를 말한다.)
보존력의 한 예로 중력이 있고, 또 다른예로 이상적인 용수철에 달린 물체에 작용하는 용수철 힘이 있다.
계의 구성 요소 사이에 작용하는 힘에 대하여 퍼텐셜 에너지를 연관시키려면, 그 힘이 보존력인 경우에만 그렇게 할 수 있따. 일반적으로 계가 한 배열 상태에서 다른 배열 상태로 변할 떄, 계의 구성 요소 중의 하나인 물체에 보존력이 한 일 \(W_{int}\)는 계의 퍼텐셜 에너지의 처음 값에서 나중 값을 뺀 것과 같다.
\[W_{int} = U_i - U_f = -\Delta U\]비보존력
앞에서의 성질1과 성질2를 만족하지 못하면 그 힘은 비보존력이다. 비보존력이 한 일은 경로에 의존한다. 계의 운동에너지와 퍼텐셜 에너지의 합을 역학적 에너지(mechanical energy)라고 정의한다.
\[E_{mech} \equiv K + U\]7.8 보존력과 퍼텐셜 에너지의 관계
일은 단지 처음과 나중 좌표에만 의존한다. 따라서 보존력이 계 내부에서 한 일이 식 7.21에서와 같이 계의 퍼텐셜 에너지 변화의 음의 값과 같은 퍼텐셜 에너지 함수(potential energy function) \(U\)를 정의할 수 있다.
입자들 사이에 보존력 \(\vec F\)가 작용하는 여러 입자로 구성된 계를 생각해보자. 또한 입자 하나가 \(x\)축을 따라 움직임에 따라 계의 배치 상태가 변하는 경우를 생각해보자. 입자가 \(x\)축을 따라 움직이는 동안 이 힘이 한 내부 일은 다음과 같다.
\[W_{int} = \int_{x_i}^{x_f} F_x dx = -\Delta U \qquad(7.26)\]여기서 \(F_x\)는 \(\vec F\)의 변위 방향 성분이다. 또한 다음과 같이 나타낼 수 있다.
\[\Delta U = U_f - U_i = -\int_{x_i}^{x_f} F_x dx \qquad (7.27)\]만약 힘의 작용점이 작은 변위 \(dx\) 만큼 움직인다면, 계의 작은 퍼텐셜 에너지 변화 \(dU\)는
\[dU = -F_xdx\]따라서 보존력은 퍼텐셜 에너지 함수와 다음과 같은 관계가 있다.
\[F_x = - \frac {dU}{dx} \qquad (7.29)\]즉 계 내부의 한 물체에 작용하는 보존력의 \(x\) 성분은 퍼텐셜 에너지의 \(x\)에 대한 미분값에 음(-)의 부호를 붙인 것과 같다.
7.9 에너지 도표와 계의 평형
(생략)